Subhankar Bhadra
Biography
Subhankar Bhadra is a Postdoctoral Scholar at the Pennsylvania State University, working under the supervision of Dr. Michael Schweinberger. Subhankar earned his Ph.D. from the North Carolina State University and received his Master's degree from the Indian Statistical Institute, Kolkata.
Research Overview
My research primarily focuses on two modern areas of statistics and machine learning: networks and causal inference. Networks are important because we live in an interconnected world and causal inference provides us the tools to understand the underlying mechanism behind observed relationships. In addition, I also have experience in application-driven projects, involving digital health data. Below, I highlight selected projects from my ongoing and past research.
Closed-form expressions for causal effects under dependent outcomes
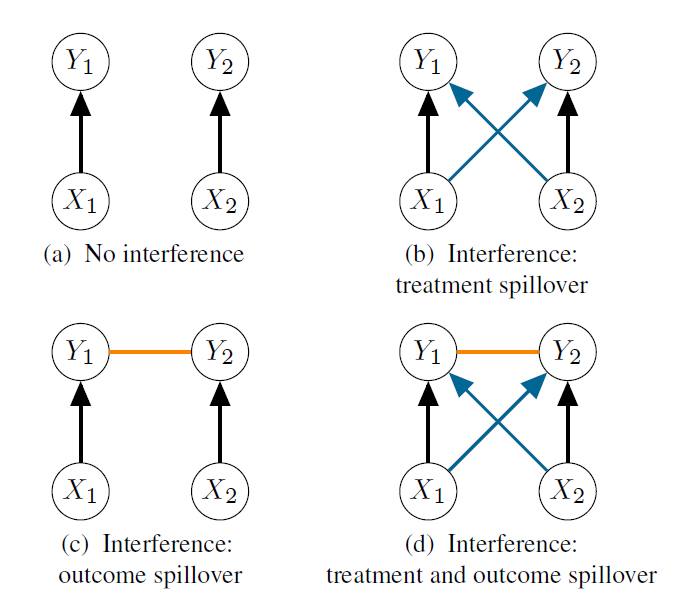Causal inference in connected populations is non-trivial, because treatment assignments and out-comes of units can affect outcomes of other units via treatment spillover and outcome spillover. Since outcome spillover induces correlations among outcomes, insight into causal inference is complicated: e.g., closed-form expressions for causal effects and rates of convergence for causal estimators based on a single observation of correlated outcomes are challenging and un-available. In Bhadra and Schweinberger (2025), we provide closed-form expressions for causal effects when treatment assignments, outcomes, and connections among units are random variables and exhibit complex dependence. The main results do not make assumptions about the joint probability law of treatment assignments, outcomes, and connections: I show that closed-form expressions for causal effects under dependence require nothing more than linearity of conditional expectations of outcomes, in addition to the standard assumptions of ignorability and positivity.
Scalable community detection in massive networks via predictive assignment
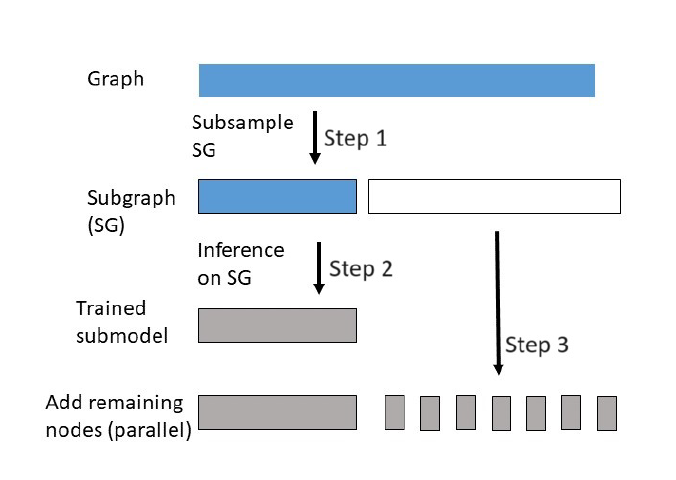Community detection is a well-known fundamental problem in network analysis. Standard community detection methods (e.g., spectral clustering, likelihood maximization) often rely on com-putationally expensive mathematical operations, such as matrix decomposition or iterative opti-mization. In today’s world, where massive networks are becoming increasingly common, it is com-putationally infeasible to perform such community detection methods in practice. I propose a strategy called predictive assignment to overcome this issue (Bhadra, Pensky, and Sengupta (2025)). In this approach, we avoid the large-scale matrix computations by applying community detection only on a small subgraph of the network to obtain the estimated communities and model parameter estimates. Then the remaining nodes are assigned to communities one by one by exploiting the mathematical structure of the model, and no clustering is needed. We prove strong consistency for predictive assignment under the stochastic block model (SBM) and its degree-corrected version (DCBM).
A unified framework for community detection and model selection in blockmodels
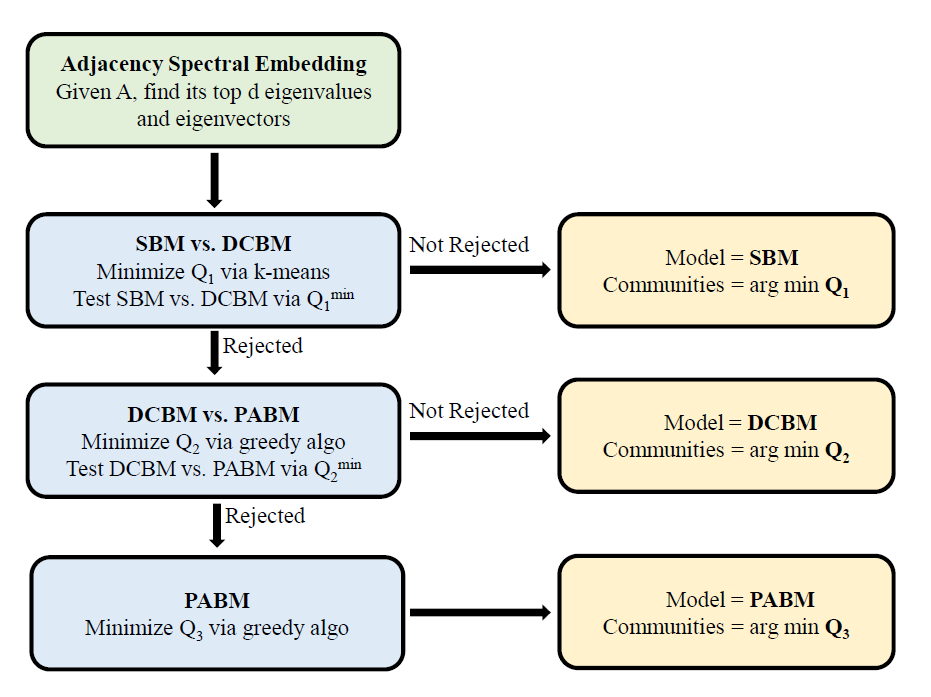Blockmodels are a foundational tool for modeling community structure in networks, with the stochastic blockmodel (SBM), degree-corrected blockmodel (DCBM), and popularity-adjusted blockmodel (PABM) forming a natural hierarchy of increasing generality. While community detection under these models has been extensively studied, much less attention has been paid to the model selection problem, i.e., determining which model best fits a given network. Building on recent theoretical insights about the spectral geometry of these models, I developed a unified framework for simultaneous community detection and model selection across the full blockmodel hierarchy (Bhadra, Tang, and Sengupta (2025)). A key innovation is the use of loss functions that serve a dual role: they act as objective functions for community detection and as test statistics for hypothesis testing. I built a greedy algorithm to minimize these loss functions and establish theoretical guarantees for exact label recovery and model selection consistency under each model.
Severity prediction of patient safety events via natural language processing
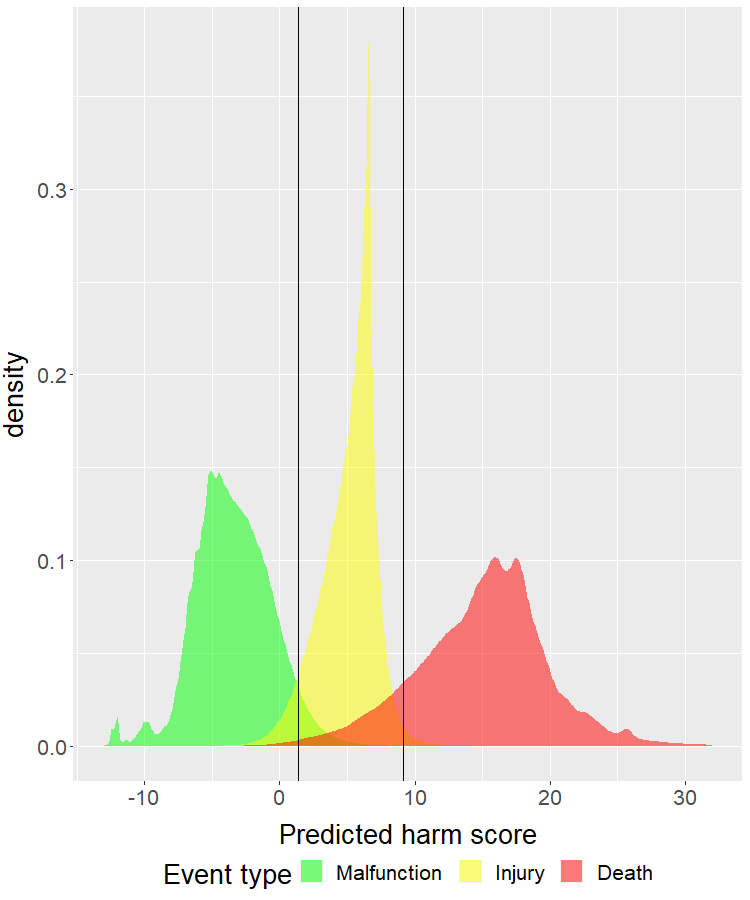Several public databases have been built to record patient safety events across healthcare systems to better understand and improve safety hazards. These reports typically include both structured fields (e.g., event type, device, manufacturer) and unstructured data elements (free text narrative of what happened). The structured fields are usually restricted to a limited number of categories, whereas the unstructured fields allow the reporter to freely describe the event details. Thus, analyzing the unstructured text, rather than the structured field, can reveal rich insights that can help improve patient safety. I present a novel application that combines NLP and statistical techniques to predict the severity level of a patient safety event based on its free text description. Training on more than 7.7 million patient safety reports from FDA’s MAUDE (Manufacturer and User Facility Device Experience) database, I built an interactive tool which (i) generates an estimated severity score for a new event report, (ii) classifies the event into one of three categories: Malfunction, Injury, or Death, and (iii) highlights key phrases driving the prediction. Feel free to try out the app with sample reports from here :)
Publications and Preprints
Bhadra, S., Tang, M., and Sengupta, S. A unified framework for community detection and model selection in blockmodels. Journal of Computational and Graphical Statistics.
https://doi.org/10.1080/10618600.2025.2590073
Fritz, C., Schweinberger, M., Bhadra, S., and D. R. Hunter. A regression framework for studying relationships among attributes under network interference. Journal of the American Statistical Association, Theory & Methods. https://doi.org/10.1080/01621459.2025.2565851
Bhadra, S., Pensky, M., and Sengupta, S. Scalable community detection in massive networks via predictive assignment. Invited major revision. Journal of the American Statistical Association, Theory & Methods. arXiv:2503.16730
Bhadra, S., and Schweinberger, M. Closed-form expressions for causal effects and rates of convergence for causal effect estimators under dependence. Under review at the Annals of Statistics. arXiv:2504.06108
Bhadra, S., and Schweinberger, M. Causal inference under network interference. Under review at Statistical Science. arXiv.2508.06808
Bhadra, S. Efficient Statistical Inference Methods for Problems in Network Science. Thesis
Teaching Experience
Instructor, STAT 415 & MATH 415, Introduction to mathematical statistics (Fall 2024).