Thursday, September 11 Dmitry Fuchs (University of California at Davis) 2:30 p.m. Is it possible to cut a tetrahedron into pieces and to assemble a cube? (Hilbert's 3rd problem) ABSTRACT: A similar question for polygons has an affirmative answer: given two polygonal domains of the same area, one can cut the first one into polygonal pieces and to assemble the second one. In dimension three, however, it is not true: the answer to the question in the title is no
! This theorem which provides an answer to one of the famous Hilbert's problems was proved by Max Dehn (actually, a year before Hilbert stated his Problems). A proof will be presented in the talk. You may think of a seemingly simpler (but, actually, almost the same) problem: is it possible to cut a 1×2 rectangle into smaller rectangles by lines, parallel to its sides, and to assemble a √2×√2 square?
Thursday, September 25 Kenneth Stephenson (University of Tennessee) 3:30 p.m. The Geometry of Spiral Circle Packings ABSTRACT: This is a talk about spontaneous
geometry—how interesting global patterns can arise from simple local rules. We start with an observation of Peter Doyle about flowers
of tangent circles: Given any positive real numbers a and b, a chain of 6 successively tangent circles of radii {a, b, b/a, 1/a, 1/b, a/b} will exactly close up around a circle of radius 1. (See the accompanying picture; find a proof.) We will see that each pair (a,b) of parameters leads to an infinite hexagonal spiral of circles in the plane, but that certain special pairs give particularly pleasing patterns. We'll end with some connections among our spirals, the golden ratio, and the seed patterns of pine cones and sunflowers. (This material is from joint work with Alan Beardon and Tomas Dubejko.) 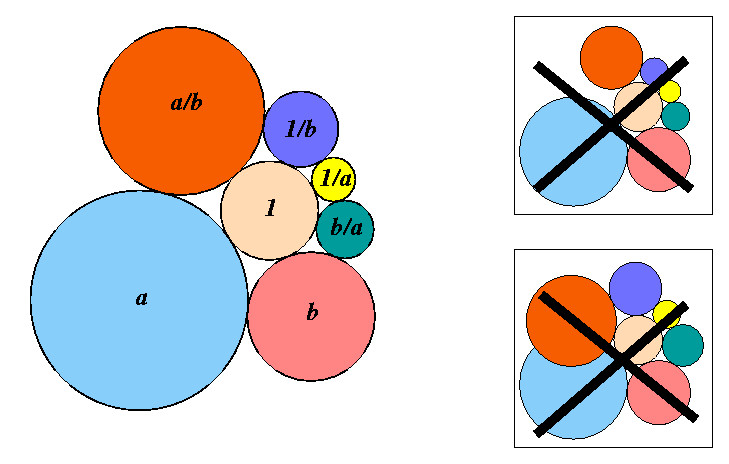
Thursday, October 2 Frank Morgan (Williams College) 2:30 p.m. Double Bubbles ABSTRACT: A single round soap bubble provides the least-area way to enclose a prescribed volume of air in R3. The recent Double Bubble Theorem (Ann. Math. 2002) says that the familiar double soap bubble provides the least-area way to enclose and separate two prescribed volumes. I'll also discuss double bubble problems in other spaces and open questions. No prerequisites.
Thursday, October 9 M. Ghomi (Georgia Tech) 3:30 p.m. Solution to the Shadow Problem in 3-Space ABSTRACT: If a convex surface, such as an egg shell, is illuminated from any direction, then the shaded area formed on the surface is a connected region. The shadow problem, formulated by H. Wente in 1978, asks whether the converse of this phenomenon is true as well, i.e., does connectedness of the shades imply the convexity of a closed surface immersed in Euclidean 3-space? In this talk we provide the answer.
Thursday, October 23 Stanley Wagon (Macalester College) 3:00 p.m. The SIAM 100 Digit Challenge: Adventures in Numerical Computing ABSTRACT
Thursday, October 30 Aaron Abrams (University of Georgia) 3:00 p.m. Braids, graphs, and robots ABSTRACT: A common technique for solving problems involving lots of moving objects is to introduce a topological space called the configuration space
associated to the problem. This talk will focus on the configuration spaces associated to motions of several points on a graph. We will play with several examples and hopefully get used to visualizing these spaces. Along the way these spaces will exhibit some neat properties, which are both mathematically interesting and useful for solving related problems in robotics.
Thursday, November 6 Krishna Alladi (University of Florida) 2:30 p.m. Irrationality measures using integration by parts ABSTRACT: Although almost all real numbers are irrational, it is generally quite difficult to establish the irrationality of a given number. The study of irrationality has a long history going back to Euclid's proof of the irrationality of the square root of 2. Proofs of irrationality which also provide irrationality measures are especially interesting. By an irrationality measure we mean a certain estimate on the quality of approximation of irrationals by rationals. Good irrationality measures for algebraic numbers can be used to show that certain Diophantine equations have only a finite number of solutions. In 1978, Roger Apery provided a startling proof of the irrationality of value of the Riemann zeta function at the integer 3, a fact that had been conjectured for a long time. Following this there was a resurgence of activity in irrationality. In this talk we will show that by just using integration by parts and properties of Legendre polynomials, we can obtain irrationality measures for values of the logarithm, π, and certain algebraic numbers.
Thursday, November 13 Hillel Furstenberg (Yale University and Hebrew University of Jerusalem) 3:00 p.m. Pascal Triangles in Modular Arithmetic, Entropy and Algebraic Functions ABSTRACT: Reading down the middle column of Pascal's triangle and reducing the terms modulo a prime we obtain a sequence of terms in a finite field whose entropy we'll determine. We're led to studying algebraic functions over finite fields, and we'll explain why we're interested in the entropy of this sequence and others like it. This will relate to the following open problem: Take a fraction bigger than 1, like 3/2, and consider its successive powers. Will these come arbitrarily close to integers?
Thursday, November 20 Kenneth Stolarsky (Uiversity of Illinois) 2:30 p.m. What do squares have to do with nim, Goldbach's conjecture, and windy planets? ABSTRACT: Sums of two squares are closed under multiplication. What about sums of N squares? A set closed under a binary associative operation is called a semigroup. Some exotic (and not obviously associative) binary operations arise in connection with the analysis of certain games. The associative operation of Minkowski addition arose (e.g.) from problems of additive number theory. These binary operations, together with the topology of flows on spheres, ultimately shed light on sums of squares. We survey this area, describe some very recent results, and display some open problems.
Thursday, December 4 Arkady Vaintrob (University of Oregon) 2:30 p.m. Fermionic Integration ABSTRACT: Fermionic integration, also known as integration over anticommuting variables, is a part of Supercalculus dealing with functions depending on ordinary, commuting (or bosonic), and odd, anticommuting (or fermionic), variables. Invented and successfully applied by physicists, it has also found important applications in various areas of Mathematics. In the talk, I will begin with a crash course in supercalculus. Then I will try to demonstrate its utility on two simple classical problems, one from linear algebra (how to find a square root of a skew-symmetric matrix) and another from graph theory (how to list all maximal trees in a given graph).
