Thursday, September 6 Alexandre Kirillov (University of Pennsylvania) 3:30 pm Family Algebras ABSTRACT: A new class of associative algebras related to simple complex Lie algebras (or root systems) was introduced in [K1] and studied in [K2]. They were named classical and quantum family algebras. I hope, it will be a useful tool in the study of semisimple Lie algebras and its representations. Consider a n×n matrix A=||aij|| whose entries are not supposed to commute. Such a matrix in general has rather unpleasant properties. In particular, its trace is not invariant under conjugation (even for n=1), it does not satisfy the Cayley-Hamilton identity 
etc… However, there are remarkable example of matrices with non-commuting entries which still satisfy an analogue of the Cayley-Hamilton identity and have so-called quantum eigenvalues λk with quantum multiplicities mk such that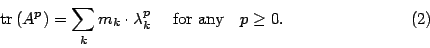 
E.g., let A=11E12E21E22 where Eij are standard matrix elements satisfying the commutation relations [Eij, Ekl] = δjkEil − δilEkj It turns out that A satisfies (1) and (2) but the multiplicities m1, m2 are not integers but some elements of the center of the algebra generated by Eij. This example find the natural explanation in terms of the family algebra associated to the standard representation of the Lie algebra gl(2). Bibliography [K1] Kirillov A.A.. Family algebras
, Electronic Research Announcements AMS (2000), Vol. 6, Issue 1. [K2] Kirillov A.A.. Introduction to Family algebras
, Moscow Journal of Mathematics (2001), Vol. 1, Issue 1, pp. 49-63.
Thursday, September 20 John Conway (Princeton University) 2:15 pm Integral Lexicographic Codes ABSTRACT: In Integral Lexicographic Codes each word is determined as the earliest possible word that is sufficiently distant from all previous ones. The Lexicode Theorem
says that Integral Lexicographic Codes are vector spaces. They lead to some surprising arithmetic.
Thursday, September 27 Augustin Banyaga (Penn State) 2:30 pm Klein's Erlanger Programme ABSTRACT: In Klein's Erlangen Programme, the GEOMETRY
of a space X is defined as the study of configurations (subsets) of X that remain invariant under a group of transformations G(X). The leitmotiv of his programme is that the group G=G(X) should be the primary object: let G act on a space X and look for invariants. To what extend then does G determine the geometry of X? We consider this problem in the realm of modern differential geometry: are topological, smooth, riemannian, unimodular, symplectic, contact, Poisson structures, etc. determined by their automorphism groups? The answer may be No (ex. riemannian structures), Yes (ex. topological smooth, unimodular, symplectic, contact structures), or unknown. The goal of this talk is to give a panoramic view of these structures and point out the properties of their automorphism groups that are pertinent to the Erlanger creed.
Thursday, October 11 V. Ovsienko (CNRS, Centre of Theoretical Physics, Luminy, France) 2:30 pm Virasoro group and projective structures on the circle: a hidden face of an old coin ABSTRACT: The Virasoro algebra and the Virasoro group are among the best gifts ever offered by mathematics to modern physics. Discovered by famous mathematicians (Gelfand-Fuchs, Thurston-Bott) and named after a physicist, they became the main characters in conformal field theory. It turns out, however, that the roots and origins of these advanced modern concepts go back to an old problem of differential geometry.
Thursday, October 18 Herman Gluck (University of Pennsylvania) 3:00 pm Vector Calculus and the Topology of Domains in 3-space ABSTRACT: Suppose you have a vector field defined on a bounded domain in 3-space. How can you tell whether your vector field is the gradient of some function? Or the curl of another vector field? Can you find a nonzero field on your domain which is divergence-free, curl-free and tangent to the boundary? How about a nonzero field which is divergence-free, curl-free and orthogonal to the boundary? To answer these questions, you need to understand the relationship between the calculus of vector fields and the topology of their domains of definition. The Hodge Decomposition Theorem provides the key by decomposing the space of vector fields on the domain into five mutually orthogonal subspaces which are topologically and analytically meaningful. This decomposition is useful not only in mathematics, but also in fluid dynamics, electrodynamics and plasma physics. The proof involves homology and cohomology theory in 3-space, and lets us see both the general Hodge theorem and the de Rham isomoprhism theorem in action.
Thursday, October 25 Alexei Sossinsky (Independent University of Moscow) 3:00 pm Minimal surfaces, discrete harmonic analysis, and random walks ABSTRACT: This lecture begins with a physical experiment (beautiful soap films spanning wire contours will be shown), but its aim is mathematical: to describe how one can compute the actual position of the film (i.e., the height of its points). This will be done by discretizing the problem and presenting two radically different (computer implementable) solutions of the discrete problem. One is based on a very natural and efficient iterative algorithm (part of a theory called discrete harmonic analysis). The other involves a model with drunkards randomly walking in cities surrounded by ditches and policemen collecting fines, but amazingly yields the same (physically correct) result as the first one, demonstrating the profound unity of completely different branches of mathematics.
Thursday, November 1 Mark Levi (Penn State University) 3:30 pm Physical proofs of mathematical theorems ABSTRACT: For millennia physics has played a key role in mathematical discovery. Archimedes, for instance, used mechanics to come up with integral calculus. Riemann was motivated by physics in a considerable part of his work. Hamilton's work on differential equations was motivated by optics. This pattern has continued into the present time with the work of Witten and others. In this talk I will describe a few (of a large number of) examples where physics makes the solution of a mathematical problem almost obvious: 1. The Gauss-Bonnet theorem 2. The Riemann Mapping Theorem 3. Moser's theorem on density uniformization
Thursday, November 8 Juan Carlos Alvarez (New York Polytechnic University) 3:00 pm One hundred years of Hilbert's fourth problem ABSTRACT: Hilbert's problems range from very concrete to totally vague. Somewhere in the middle is his fourth problem: find and study all metrics on the plane for which the shortest connection is the line segment. In this talk I will survey the progress on the solution of this problem from the early works of Busemann, Pogorelov, and Ambartzumian to recent works that relate these metrics to symplectic geometry and the study of minimal surfaces in Finsler spaces.
Thursday, November 29 Bruce Solomon (Indiana University) 3:30 pm Loops in R3: New Angles on an Old Topic ABSTRACT: Smooth loops in 3-space have been studied since the beginnings of calculus, and the Frenet-Serret formulae go back to the mid-19th century. Even so, two recent investigations reveal new kinds of results about these simple classical objects. The first concerns loops having no pair of parallel tangent lines. These skewloops, so-named in a recent work with M. Ghomi and S. Tabachnikov, exhibit an interesting aversion to quadrics. A second set of results pertains to oriented loops which project to zero
in several independent directions. We will explain this terminology and show that one can construct such loops on convex, but not on strictly convex surfaces.